A deceptively simple experiment that involves making precise measurements of the time it takes for a particle to go from point A to point B could cause a breakthrough in quantum physics. The findings could focus attention on an alternative to standard quantum theory called Bohmian mechanics, which posits an underworld of unseen waves that guide particles from place to place.
A new study, by a team at the Ludwig Maximilian University of Munich (L.M.U.) in Germany, makes precise predictions for such an experiment using Bohmian mechanics, a theory formulated by theoretical physicist David Bohm in the 1950s and augmented by modern-day theorists. Standard quantum theory fails in this regard, and physicists have to resort to assumptions and approximations to calculate particle transit times. “If people knew that a theory that they love so much—standard quantum mechanics—cannot make [precise] predictions in such a simple case, that should at least make them wonder,” says theorist and L.M.U. team member Serj Aristarhov.
It is no secret that the quantum world is weird. Consider a setup in which an electron gun fires the subatomic particles at a screen, as in the classic “double-slit experiment” [see graphic below]. You cannot predict exactly where any given electron will land to form, say, a fluorescent dot. But you can predict with precision the spatial distribution, or pattern, of dots that takes shape over time as the electrons land one by one. Some locations will have more electrons; others will have fewer. But this weirdness hides something even stranger. All else being equal, each electron will reach the detector at a slightly different time, its so-called arrival time. Just like the positions, the arrival times will have a distribution: some arrival times will be more common, and others will be less so. Textbook quantum physics has no mechanism for precisely predicting this temporal distribution. “Normal quantum theory is concerned only with ‘where’; they ignore the ‘when,’” says team member and theorist Siddhant Das. “That’s one way to diagnose that there’s something fishy.”
There is a deep reason for this curious shortcoming. In standard quantum theory, a physical property that can be measured is called an observable. The position of a particle, for example, is an observable. Each and every observable is associated with a corresponding mathematical entity called an operator. But the standard theory has no such operator for observing time. In 1933 Austrian theoretical physicist Wolfgang Pauli showed that quantum theory could not accommodate a time operator, at least not in the standard way of thinking about it. “We conclude therefore that the introduction of a time operator ... must be abandoned fundamentally,” he wrote.
Yet measuring particle arrival times, or their “time of flight,” is an important part of experimental physics. Detectors at CERN’s Large Hadron Collider, for example, and instruments called mass spectrometers use such measurements to calculate the masses and momenta of particles, ions and molecules. There is, however, a serious wrinkle: although these calculations concern quantum systems, they cannot be made using unadulterated quantum mechanics. Instead they require assumptions. In one method, for example, experimenters assume that once the particle leaves its source, it behaves classically, meaning it follows Newton’s equations of motion.
The result is a hybrid approach—one that is part quantum, part classical. It starts with the quantum perspective, in which each particle is represented by a mathematical abstraction called a wave function. Identically prepared particles will have identical wave functions when they are released from their source. But measuring the momentum of each particle (or, for that matter, its position) at the instant of release will yield different values each time. Taken together, these values follow a distribution that is precisely predicted by the initial wave function. Starting from this ensemble of values for identically prepared particles and assuming that a particle follows a classical trajectory once it is emitted, the result is a distribution of arrival times at the detector that depends on the initial momentum distribution.
Standard theory is also often used for another quantum-mechanical method for calculating arrival times. As a particle flies toward a detector, its wave function evolves according to the Schrödinger equation, which describes a particle’s changing state over time. Consider the one-dimensional case of a detector that is a certain horizontal distance from an emission source. The Schrödinger equation determines the wave function of the particle—and hence the probability of detecting that particle at that location—assuming that the particle crosses the location only once. (There is, of course, no clear way to substantiate this assumption in standard quantum mechanics.) Using such assumptions, physicists can calculate the probability that the particle will arrive at the detector at a given time (t) or earlier. “From the perspective of standard quantum mechanics, it sounds perfectly fine,” Aristarhov says. “And you expect to have a nice answer from that.”
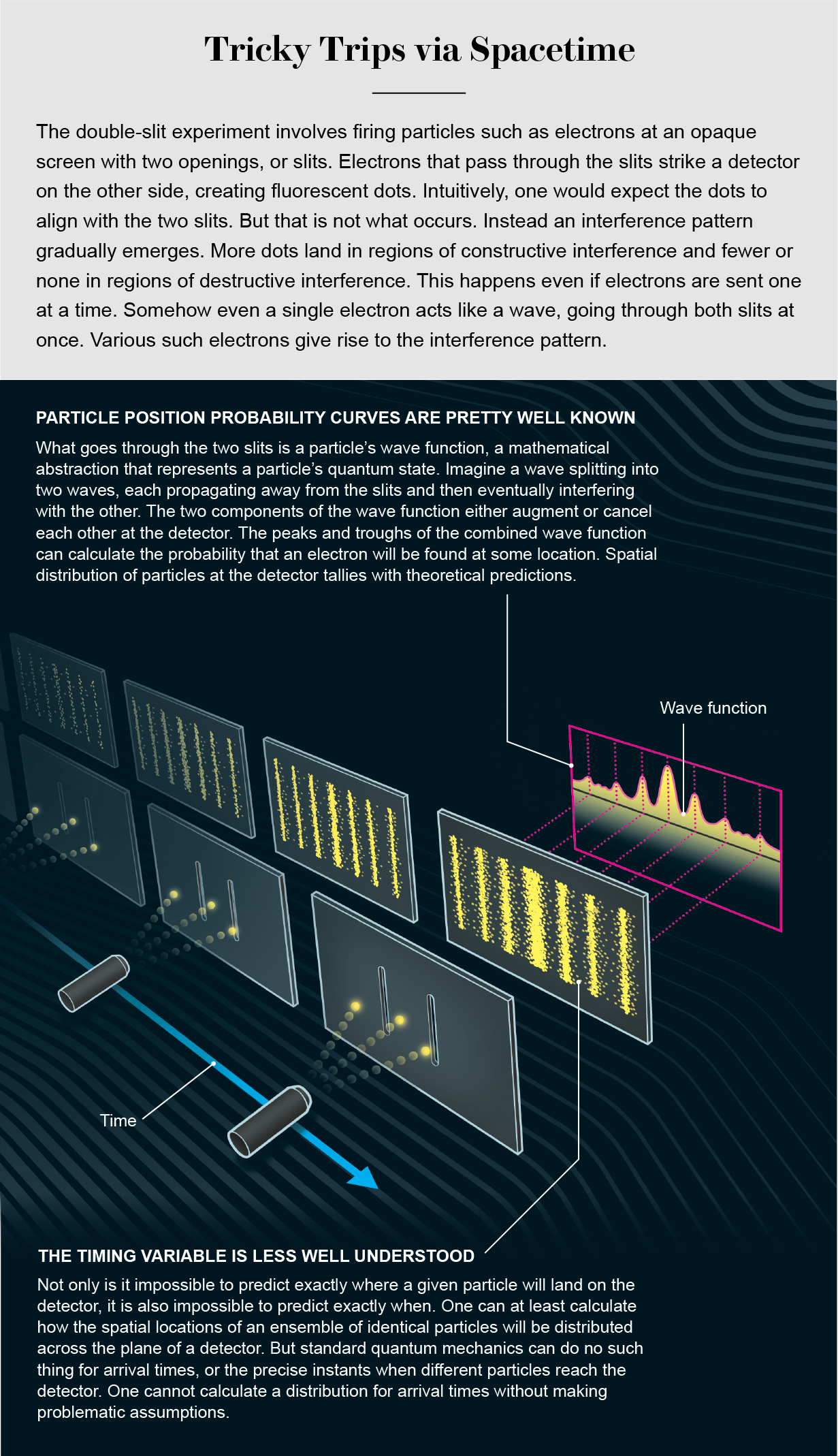
There is a hitch, however. To go from the probability that the arrival time is less than or equal to t to the probability that it is exactly equal to t involves calculating a quantity that physicists call the quantum flux, or quantum probability current—a measure of how the probability of finding the particle at the detector location changes with time. This works well, except that at times the quantum flux can be negative. Even though it is hard to find wave functions for which the quantity becomes appreciably negative, nothing “prohibits this quantity from being negative,” Aristarhov says. “And this is a disaster.” A negative quantum flux leads to negative probabilities, and probabilities can never be less than zero.
Using the Schrödinger evolution to calculate the distribution of arrival times works only when the quantum flux is positive—a case that, in the real world, only definitively exists when the detector is in the “far field,” or at a considerable distance from the source, and the particle is moving freely in the absence of potentials. When experimentalists measure such far-field arrival times, both the hybrid and quantum-flux approaches make similar predictions that tally well with experimental findings. But they do not make clear predictions for “near field” cases, where the detector is very close to the source.
Bohmian Predictions
In 2018 Das and Aristarhov, along with their then Ph.D. adviser Detlef Dürr, an expert on Bohmian mechanics at L.M.U., who died in 2021, began working with colleagues on Bohmian-based predictions of arrival times. Bohm’s theory holds that each particle is guided by its wave function. Unlike standard quantum mechanics, in which a particle is considered to have no precise position or momentum prior to a measurement—and hence no trajectory—particles in Bohmian mechanics are real and have squiggly trajectories described by precise equations of motion (albeit ones that differ from Newton’s equations of motion).
Among the researchers’ first findings was that far-field measurements would fail to distinguish between the predictions of Bohmian mechanics and those of the hybrid or quantum-flux approaches. This is because over large distances Bohmian trajectories become straight lines, so the hybrid semiclassical approximation holds. Also, for straight far-field trajectories, the quantum flux is always positive, and its value is predicted exactly by Bohmian mechanics. “If you put a detector far enough [away] and you do Bohmian analysis, you see that it coincides with the hybrid approach and the quantum-flux approach,” Aristarhov says.
The key, then, is to do near-field measurements—but those have long been considered impossible. “The near-field regime is very volatile,” Das says. “It’s very sensitive to the initial wave-function shape you have created.” Also, “if you come very close to the region of initial preparation, the particle will just be detected instantaneously. You cannot resolve [the arrival times] and see the differences between this prediction and that prediction.”
To avoid this problem, Das and Dürr proposed an experimental setup that would allow particles to be detected far away from the source while still generating unique results that could distinguish the predictions of Bohmian mechanics from those of the more standard methods.
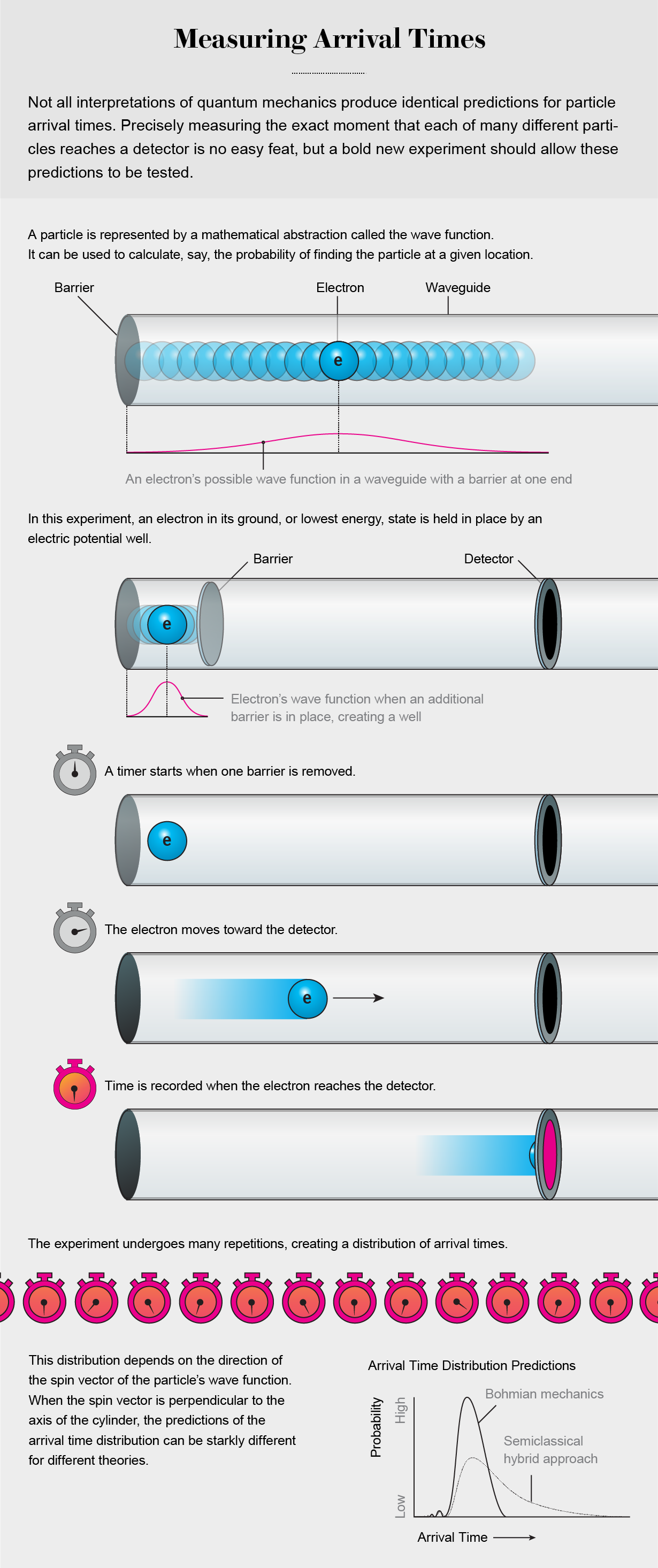
Conceptually, the team’s proposed setup is simple. Imagine a waveguide—a cylindrical pathway that confines the motion of a particle (an optical fiber is such a waveguide for photons of light, for example). On one end of the waveguide, prepare a particle—ideally an electron or some particle of matter—in its lowest energy, or ground, state and trap it in a bowl-shaped electric potential well. This well is actually the composite of two adjacent potential barriers that collectively create the parabolic shape. If one of the barriers is switched off, the particle will still be blocked by the other that remains in place, but it is free to escape from the well into the waveguide.
Das pursued the painstaking task of fleshing out the experiment’s parameters, performing calculations and simulations to determine the theoretical distribution of arrival times at a detector placed far away from a source along a waveguide’s axis. After a few years of work, he had obtained clear results for two different types of initial wave functions associated with particles such as electrons. Each wave function can be characterized by something called its spin vector. Imagine an arrow associated with the wave function that can be pointing in any direction. The team looked at two cases: one in which the arrow points along the axis of the waveguide and another in which it is perpendicular to that axis.
The team showed that when the wave function’s spin vector is aligned along the waveguide’s axis, the distribution of arrival times predicted by the quantum-flux method is identical to that predicted by Bohmian mechanics. But these distributions differ significantly from those calculated for the hybrid approach. When the spin vector is perpendicular, the distinctions become even starker. With help from their L.M.U. colleague Markus Nöth, the researchers showed that all the Bohmian trajectories will strike the detector at or before this cutoff time. “This was very unexpected,” Das says.
Again, the Bohmian prediction differs significantly from the predictions of the semiclassical hybrid theory, which do not exhibit such a sharp arrival-time cutoff. And crucially, in this scenario, the quantum flux is negative, meaning that calculating arrival times using Schrödinger evolution becomes impossible. The standard quantum theorists “put their hands up when [the quantum flux] becomes negative,” Das says. But Bohmian mechanics continues to make predictions. “There’s a clear distinction between [it] and everything else,” Aristarhov says.
Experimentalists Enter the Fray
Quantum theorist Charis Anastopoulos of the University of Patras in Greece, an expert on arrival times, who was not involved with this work, is both impressed and circumspect. “The setup they are proposing seems plausible,” he says. And because each approach to calculating the distribution of arrival times involves a different way of thinking about quantum reality, a clear experimental finding could jolt the foundations of quantum mechanics. “It will vindicate particular ways of thinking,” Anastopoulos says. “So in this way, it will have some impact.... If it [agrees with] Bohmian mechanics, which is a very distinctive prediction, this would be a great impact, of course.”
At least one experimentalist is gearing up to make the team’s proposal a reality. Before Dürr’s death, Ferdinand Schmidt-Kaler of the Johannes Gutenberg University Mainz in Germany had been in discussions with him about testing arrival times. Schmidt-Kaler is an expert on a type of ion trap in which electric fields are used to confine a single calcium ion. An array of lasers is used to cool the ion to its quantum ground state, where the momentum and position uncertainties of the ion are at their minimum. The trap is a three-dimensional bowl-shaped region created by the combination of two electric potentials; the ion sits at the bottom of this “harmonic” potential. Switching off one of the potentials creates conditions similar to what is required by the theoretical proposal: a barrier on one side and a sloping electric potential on the other side. The ion moves down that slope, accelerates and gains velocity. “You can have a detector outside the trap and measure the arrival time,” Schmidt-Kaler says. “That is what made it so attractive.”
For now his group has done experiments in which the researchers eject the ion out of its trap and detect it outside. They showed that the time of flight is dependent on a particle’s initial wave function. The results were published in 2021 in the New Journal of Physics. Schmidt-Kaler and his colleagues have also performed not yet published tests of the ion exiting the trap only to be reflected back in by an “electric mirror” and recaptured—a process the setup achieves with 98 percent efficiency, he says. “We are underway,” Schmidt-Kaler says. “Of course, it is not tuned to optimize this measurement of the time-of-flight distribution, but it could be.”
That is easier said than done. The detector outside the ion trap will likely be a sheet of laser light, and the team will have to measure the ion’s interaction with the light sheet to nanosecond precision. The experimentalists will also need to switch off one half of the harmonic potential with similar temporal precision—another serious challenge. These and other pitfalls abound on the path between theoretical prediction and experimental realization.
Still, Schmidt-Kaler is excited about the prospect of using time-of-flight measurements to test the foundations of quantum mechanics. “This has the attraction of being completely different from other [kinds of] tests. It really is something new,” he says. “This will go through many iterations. We will see the first results, I hope, in the next year. That’s my clear expectation.” Meanwhile Aristarhov and Das are reaching out to others, too. “We really hope that the experimentalists around the world notice our work,” Aristarhov says. “We will join forces to do the experiments.”
In a yet to be published paper co-authored by Dürr before he died, the closing words could almost be an epitaph: “It should be clear by now that the chapter on time measurements in quantum physics can only be written if genuine quantum-mechanical time-of-flight data become available.” Which theory will the experimental data pick out as correct—if any? As Dürr wrote, “It’s a very exciting question.”

