It does something to you when you drive in here for the first time,” Enrico Calloni says as our car bumps down into the tunnel of a mine on the Italian island of Sardinia. After the intense heat aboveground, the contrast is stark. Within seconds, damp, cool air enters the car as it makes its way into the depths. “I hope you're not claustrophobic.” This narrow tunnel, which leads us in almost complete darkness to a depth of 110 meters underground, isn't for everyone. But it's the ideal site for the project we are about to see—the Archimedes experiment, named after a phenomenon first described by the ancient Greek scientist, which aims to weigh “nothing.”
The car stops, and our driver, Luca Loddo, gets out and equips everyone with helmets and flashlights. We cover the last part of the trip on foot, deeper and deeper into the tunnel. We pass a door to a room where seismographs record the subtle movements of the surrounding earth. Finally, a cave appears on the left side of the tunnel, with a spotlight pointing at it, and we stop. “This is where it's supposed to take place,” explains Calloni, a physicist at the Italian National Institute of Nuclear Physics.
Geologically, Sardinia is one of the quietest places in Europe. The island, along with its neighbor Corsica, is located on a particularly secure block of Earth's crust that is among the most stable areas of the Mediterranean, with very few earthquakes in its entire recorded history and only one (offshore) event that ever reached the relatively mild category of magnitude 5. Physicists chose this geologically uneventful place because the Archimedes experiment requires extreme isolation from the outside environment. It involves a high-precision experimental setup designed to investigate the worst theoretical prediction in the history of physics—the amount of energy in the empty space that fills the universe.
Researchers can calculate the energy of the vacuum in two ways. From a cosmological perspective, they can use Albert Einstein's equations of general relativity to calculate how much energy is needed to explain the fact that the universe is expanding at an accelerated rate. They can also work from the bottom up, using quantum field theory to predict the value based on the masses of all the “virtual particles” that can briefly arise and then disappear in “empty” space (more on this later). These two methods produce numbers that differ by more than 120 orders of magnitude (1 followed by 120 zeros). It's an embarrassingly absurd discrepancy that has important implications for our understanding of the expansion of the universe—and even its ultimate fate. To figure out where the error lies, scientists are hauling a two-meter-tall cylindrical vacuum chamber and other equipment down into an old Sardinian mine where they will attempt to create their own vacuum and weigh the nothing inside.
What's in Empty Space?
A vacuum is not completely empty. This is because of an idea in quantum physics called Heisenberg's uncertainty principle. The principle states that you can't determine the position and the velocity of a particle at the same time with any precision—the more precisely you know one value, the less precisely you can know the other. This principle also applies to other measurements, such as those involving energy and time. Its consequences are considerable. It means that nature can “borrow” energy for extremely short amounts of time. These changes in energy, known as vacuum fluctuations, often take the form of virtual particles, which can appear out of nowhere and disappear again immediately.

Vacuum fluctuations have to respect some rules. A single electrical charge, for example, cannot suddenly appear where there was none (this would violate the law of charge conservation). This means that only electrically neutral particles such as photons can pop out of the vacuum by themselves. Electrically charged particles have to emerge paired with their antiparticle matches. An electron, for instance, can appear along with a positron, which is positively charged; the two charges cancel each other out to preserve the total charge of zero. The result is that the vacuum is continuously filled with a stream of short-lived particles buzzing around.
Even if we can't capture these virtual particles in detectors, their presence is measurable. One example is the Casimir effect, predicted by Dutch physicist Hendrik Casimir in 1948. According to his calculations, two opposing metal plates should attract each other in a vacuum, even without taking into account the slight gravitational pull they exert on each other. The reason? Virtual particles. The presence of the plates imposes certain limits on which virtual particles can emerge from the vacuum. For example, photons (particles of light) with certain energies can't appear between the plates. That's because the metal plates act like mirrors that reflect the photons back and forth. Photons with certain wavelengths will end up with wave troughs overlapping wave crests, effectively canceling themselves out. Other wavelengths will be amplified if two wave peaks overlap. The result is that certain energies are preferred, and others are suppressed as if those photons were never there. This means that only virtual particles with certain energy values can exist between the plates. Outside them, however, any virtual particles can emerge.
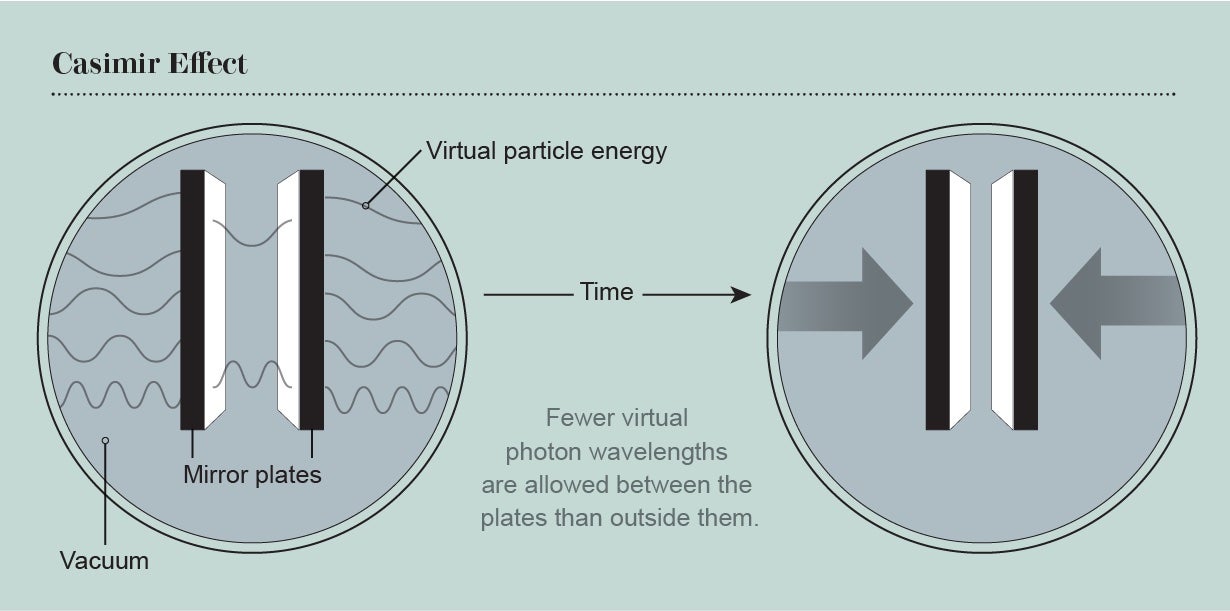
The result is that there are fewer possibilities—and therefore fewer virtual particles—between the plates than around them. The comparative abundance of particles on the outside exerts pressure on the plates, pressing them together. This effect, strange as it may sound, is measurable. Physicist Steven Lamoreaux confirmed the phenomenon experimentally at the University of Washington in 1997, almost 50 years after Casimir's prediction. Now Calloni and his colleagues hope to use the Casimir effect to measure the energy of the void.
This energy has important consequences for the universe as a whole. General relativity tells us that energy (for example, in the form of mass) curves spacetime. That means virtual particles, which change the energy of the vacuum for a short time, have an effect on the shape and the development of our universe. When this connection first became clear, cosmologists hoped it would solve a major puzzle in their field: the value of the cosmological constant, another way of describing the energy in empty space.
The Cosmological Constant
Einstein published his general theory of relativity in 1915, but he soon realized he had a problem. The theory seemed to predict an expanding universe, yet astronomers at the time believed that our cosmos was static: that space had a fixed, unchanging size.
Three years after he published the theory, Einstein found that he could add a term called the cosmological constant to his equations without changing the fundamental laws of physics. Given the right value, this term would ensure that the universe neither expands nor contracts. In the 1920s, however, astronomer Edwin Hubble used the largest telescope of the time, the Hooker telescope at Mount Wilson Observatory in California, to observe that the farther away a galaxy was from Earth, the faster it seemed to be receding. This trend revealed that space was, in fact, expanding. Einstein discarded the cosmological constant, calling it “folly.”

More than half a century later there was another twist: By observing distant supernovae, two research teams independently proved that the universe isn't just expanding—it's doing so at an accelerated rate. The force that pushes space apart has since been called dark energy. It acts as a kind of counterpart to gravity, preventing all massive objects from eventually collapsing into one place. According to theoretical predictions, dark energy accounts for about 68 percent of the total energy in space. At this point, the cosmological constant came back into fashion as a possible explanation for this mysterious form of energy. And the cosmological constant, in turn, is thought to get its energy from the vacuum.
At first, the scientific community was delighted: it seemed that general relativity's constant was the result of the energy of virtual particles in empty space. Two different fields of physics—relativity and quantum theory—were coming together to explain the accelerated expansion of the universe. But the joy didn't last long. When scientists did the two calculations, the energy of the vacuum based on quantum field theory turned out to be much larger—120 orders of magnitude higher—than the value of the cosmological constant astronomers derived from measuring the universe's expansion. The best way to resolve the discrepancy would be to measure the energy present in the vacuum directly—by weighing virtual particles.
A Scale for the Universe
If the vacuum energy derived from quantum theory is correct, then something must be stifling this energy's effects on the expansion of space. If this value were the true strength of dark energy, space would be ballooning much, much faster. If, on the other hand, the value from cosmology is right, then physicists are vastly overestimating how much energy virtual particles contribute to the vacuum.
That vacuum fluctuations and virtual particles exist has been widely accepted at least since the Casimir effect was demonstrated. And quantum theory's predicted strength for the fluctuations can't be completely off, either, because laboratory experiments confirm the theory to great precision. But might it be possible that virtual particles don't actually gravitate the way we think and therefore don't affect the weight of space as we tend to expect?
So far no direct measurements have ever been made of how virtual particles behave with respect to gravity. And some scientists have suggested they may interact with gravity differently than ordinary matter does. For instance, in 1996 physicists Alexander Kaganovich and Eduardo Guendelman of Ben-Gurion University in Israel worked out a theoretical model in which the fluctuations of the vacuum have no gravitational effect. This might be the case if there are extra dimensions beyond the regular three of space and one of time that we're familiar with. These hidden dimensions might modify the behavior of gravity on very small scales.

Yet mass differences in atomic nuclei of elements such as aluminum and platinum can be explained only if certain quantum fluctuations contribute to their weight. That's why many physicists are convinced virtual particles interact with gravity just as ordinary particles do. “There are clear indications of this but so far no direct proof,” says theoretical physicist Carlo Rovelli, who was involved in the Archimedes experiment's theoretical planning.
To verify that virtual particles interact with gravity like normal matter, the Archimedes team members want to use the Casimir effect to weigh virtual particles with a simple beam balance. The balance will sit inside their vacuum chamber, a cylindrical container of “nothing” that will be nested in several layers of insulation to keep it extremely cold and protected from the outside environment. Those layers, in turn, will sit deep inside the Sardinian cave, protecting the delicate apparatus from every possible influence of the aboveground world. These barriers are necessary because the scientists are searching for a minute signal: the slight movement of the balance when the Casimir effect turns on, changing the weight of a sample material by altering the population of virtual particles inside it. “In principle, we have known the basic principles needed for this for decades,” explains postdoctoral researcher Luciano Errico, a member of the experiment team. “I wondered myself at first why it took so long to tackle this task.”
In 1929 physicist Richard Tolman wondered if certain forms of energy (he focused on heat) could be weighed. Seven decades later Calloni thought about pushing the idea forward. After reading a technical paper by the late physicist Steven Weinberg, he envisioned weighing the gravitational contribution of virtual particles using Archimedes' principle, which states that when a body is immersed in fluid, it experiences an upward buoyant force equal to the weight of the fluid that the body displaces. If virtual particles have weight, then a cavity of metal plates in a vacuum should experience a buoyant force. The cavity is essentially displacing the regular vacuum, with its abundant virtual particles, with a lighter vacuum containing fewer virtual particles. Determining the strength of the buoyant force, which depends on the density of the virtual particles, will reveal their weight.
To measure this force within their vacuum tube, the researchers will suspend two samples made of different materials from a two-meter-tall, 1.50-meter-wide balance and induce the Casimir effect within one. To do this, they will heat both materials at regular intervals by about four degrees Celsius and then cool them down again. This temperature difference is sufficient for one of the samples to switch back and forth between a superconducting phase (when electricity flows freely within the material) and an insulating phase (when electricity cannot easily flow). The other material, however, always remains an insulator. As the conductivity changes in the first sample, it acts like the classic two-plate setup, and the number of possible virtual particles within it varies. Thus, the buoyancy force periodically increases and decreases on the first weight. This variation should cause the balance to oscillate at regular intervals, like a seesaw with two children sitting on it.
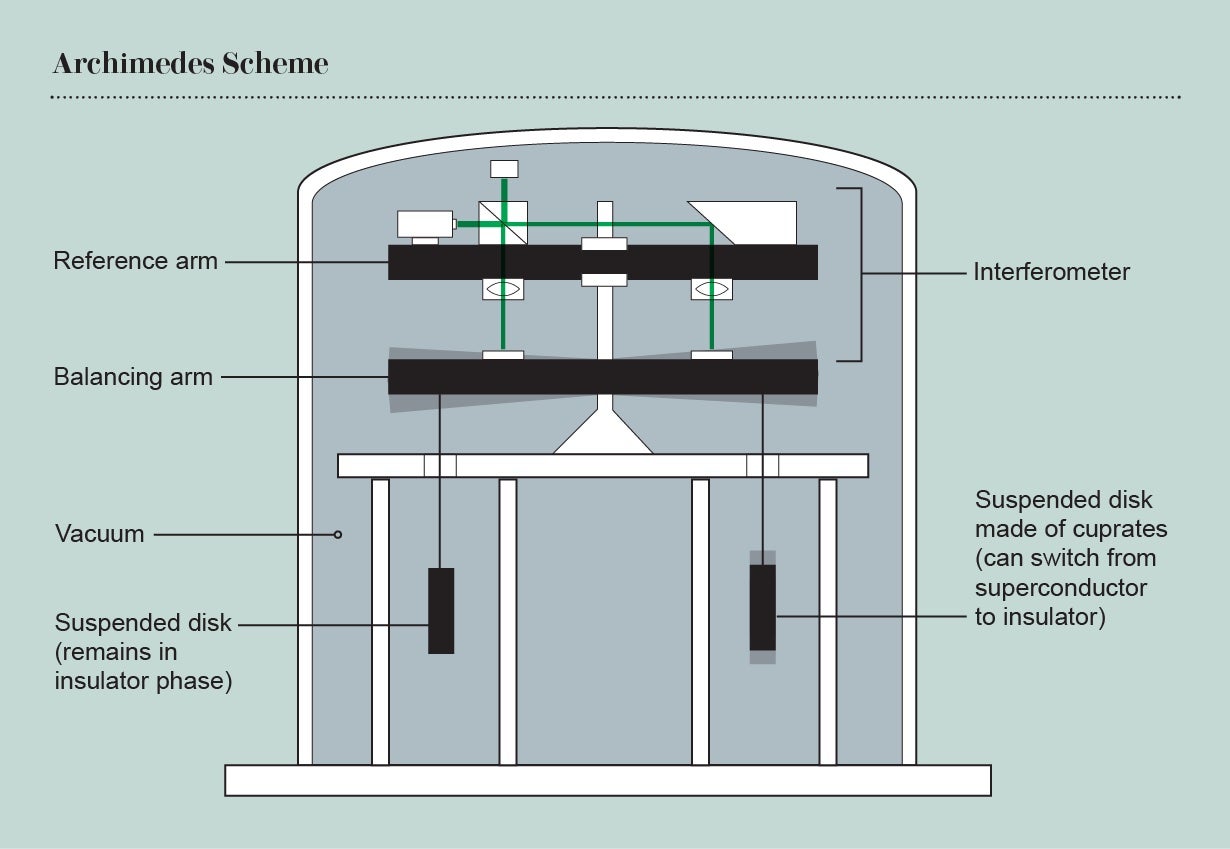
In planning the experiment, the scientists needed to find a suitable material that could be heated and cooled uniformly and quickly and that exhibited a strong Casimir effect. After considering several options, the team chose superconducting crystals called cuprates. The resulting samples are disks with a diameter of about 10 centimeters that are only several millimeters thick. To date, no one has proved that the Casimir effect works in high-temperature superconductors, but the scientists are betting that it does.
The researchers have rigged the balance so that it hangs freely in space within its vacuum chamber, which will cool the entire apparatus to less than 90 kelvins (just under –180 degrees Celsius). The chamber itself will be packed into two larger metal containers—one canister filled with liquid nitrogen, within another airless container, which acts like a thermos. Without that final cocoon, the second layer would heat up too quickly. The entire structure will be about three meters high, wide and deep and will weigh several tons.
A Sensitive Signal
Calloni began working with colleagues in 2002 to develop a theoretical model to calculate the strength of the buoyancy force for different experimental setups. They found the force in a realistic experiment would be about 10–16 newton. Measuring such a tiny force is like trying to weigh the DNA in a cell. “The numbers are devastating,” says physicist Ulf Leonhardt of the Weizmann Institute of Science in Rehovot, Israel. “On the other hand, 10 years ago hardly anyone believed gravitational waves could now be detected.”

In fact, the technology in today's gravitational-wave detectors, which first observed their target in 2015, could help detect the tiny gravitational signals the Archimedes experiment seeks. Calloni himself was involved in building the Italian gravitational-wave detector VIRGO. “It is only because of the extremely sensitive instruments made for precision measurements of gravitational waves that all this is possible,” Errico says.
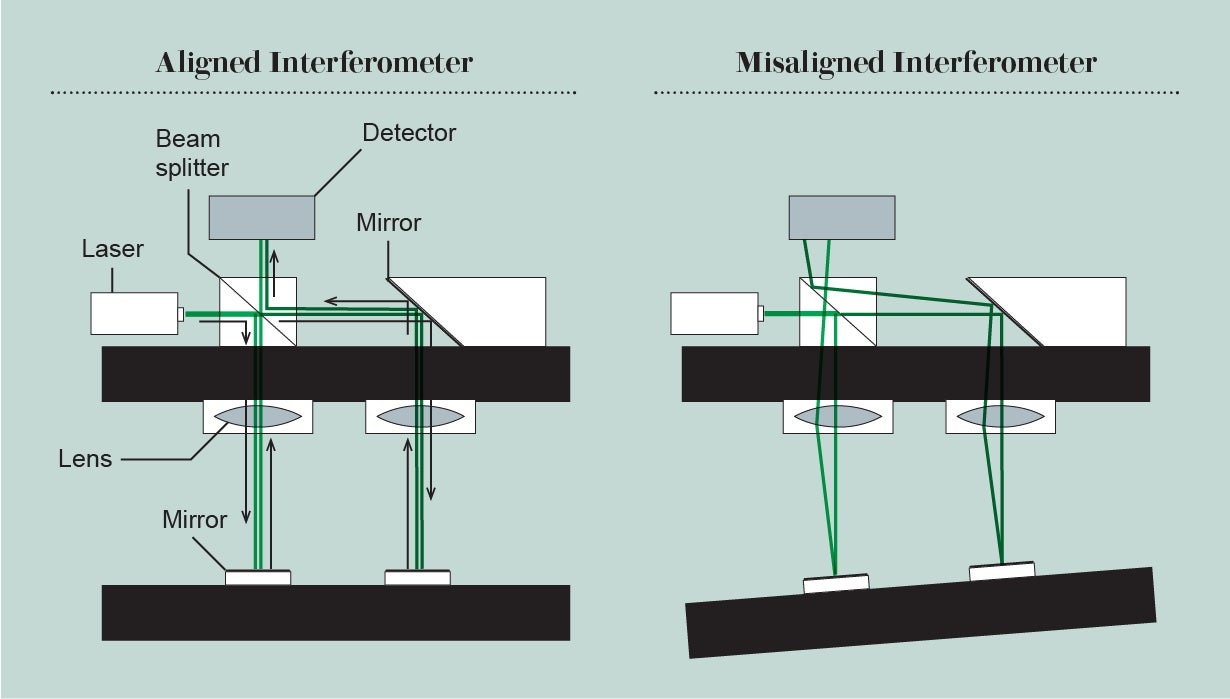
To be able to detect the minuscule deflections it seeks, the Archimedes experiment will use two laser systems that share some similarities with the laser-and-mirrors setups within gravitational-wave detectors. The first splits a laser beam in two by directing it through a beam splitter to both ends of the scale, where they are reflected by attached mirrors. The beams are then recombined by further mirrors and travel to a detector. If the beam is in balance, the two beams will travel exactly the same distance. If the arm is slightly tilted in one direction, the beams will cover different distances. In that case, the crests and troughs of the laser beam waves will meet in the measuring device in a staggered manner, producing a different intensity. This system can detect even the smallest deviations from equilibrium.
A second set of lasers measures the direction of the tilt if there is a large movement. A simplified prototype of the experiment that operates at room temperature is already remarkably sensitive, boding well for the final Archimedes apparatus's performance. But even with such sophisticated measurement systems, implementing the experiment will be difficult. “In experiments like this, the whole world works against you,” says physicist Vivishek Sudhir of the Massachusetts Institute of Technology.
To shield the balance from the outside world, the physicists needed a site with as little seismic activity as possible—hence Sardinia. The island has other advantages. It's not too densely populated, which keeps human-made noise low. It also has more than 250 abandoned mines, many of them no longer in use, which are appealing because there are even fewer vibrations underground and because the temperature inside a mine is especially stable.
Eventually the team fixed on the Sos Enattos mine on the east side of the island, which has been closed since the 1990s. The mine has a long history: in ancient times, the Romans used it to extract silver and zinc ores. Today Loddo, our driver for the trip, is responsible for the shafts; he had previously worked as a technician in the mine. “Just before it was closed, there were only about 30 people working there,” Loddo says as he walks us through the mine. “They then took care of converting the underground passages so that they could be used as a museum.” A few years later he took over the mine's management and organized guided tours. In some areas, there are still educational installations depicting the different steps miners took in their work: here a figure filling a cart with rocks, there someone attaching explosives to a wall, and elsewhere an elaborate replica of a worker operating a pneumatic drill. “Today the mine is used only for scientific operations,” Loddo explains.
The room where they plan to do the experiment looks more like an archaeological site than a laboratory, with its high walls of unadorned stone and vaulted cave ceiling. “The whole room has already been enlarged quite a bit, but there is still a lot of work to be done,” Calloni says. The room still has to get bigger, for example. It needs a ventilation shaft, a proper floor, and more.
The final version of the balance setup was recently completed and shipped to Sardinia. The vacuum chamber is at the test site, but its two outer envelopes are still in production. When they arrive and when the cave is ready, scientists will move the entire setup to this dark underground room and start running real trials.
It's been a long process to get to this point. “It took me about six months to plan the setup in detail,” Errico says. “Where should which adjusting screw go? What does the ideal beam splitter look like, and where do you position it? It then took about a year for all the parts to arrive and for me to put it together.” And the calibration to get the laser to hit all the fixtures accurately? “That actually only took 30 minutes. I had planned everything so precisely that there were only a few degrees of freedom. When everything really worked out the way I had imagined, I almost cried with joy.”
Precision Measurements
Despite the team's careful planning, the measurement will be quite challenging, says Lamoreaux, who first demonstrated the Casimir effect. “I have long dreamed of measuring the Casimir force between superconducting plates,” he says. “But making a suitable sample was beyond my capabilities.”
The experiment's precision measurements would have to be a factor of 10 better than the best gravitational-wave detectors operating today, points out Karsten Danzmann, director of the Max Planck Institute for Gravitational Physics in Hannover, Germany. He finds the project fascinating but ambitious.

If it works, though, the results will have major consequences. “The experiment is extremely important,” Leonhardt says, “because it would prove that vacuum fluctuations are indeed a real quantity with a gravitational contribution.” If the measurements match expectations and show that virtual particles interact gravitationally just like ordinary matter, then we will know for sure that vacuum fluctuations must affect Einstein's general relativity equations. Consequently, they probably have very strong effects. In that case, cosmologists will have to explain what suppresses the influence of vacuum energy in the universe.
If the deflections of the balance turn out differently than expected, it might mean several things. On the one hand, such a result could open the door to entirely new physics if it showed that virtual particles don't gravitate. But “a missing signal could also be because there is no Casimir effect in cuprates, or it is very weak,” says experimental physicist Markus Aspelmeyer of the University of Vienna. “Therefore, it is even more important to test separately from this experimentally.”
The Archimedes researchers themselves aren't making any predictions. “We don't want to formulate a hypothesis yet, so as not to falsify the experiment,” Calloni says. “But whatever result we get, it will definitely be exciting.”


